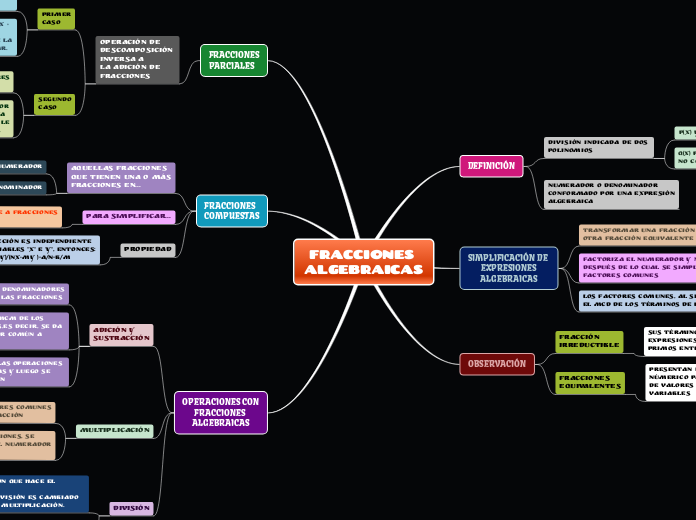
FRACCIONES
ALGEBRAICAS
OPERACIONES CON
FRACCIONES
ALGEBRAICAS
DIVISIÓN
Luego se procede como el caso
anterior
Se invierte la fracción que hace el divisor
y el operador de la división es cambiado
por el operador de la multiplicación.
MULTIPLICACIÓN
Realizadas las simplificaciones, se
multiplica lo que queda del numerador
y lo del denominador
Verifica si existen factores comunes
en los términos de la fracción
ADICIÓN Y
SUSTRACCIÓN
Efectúan las operaciones
respectivas y luego se
simplifican
Determina el MCM de los
denominadores,es decir, se da
un denominador común a
las fracciones
Factorizan los denominadores
de cada una de las Fracciones
FRACCIONES
COMPUESTAS
PROPIEDAD
Si una fracción es independiente
de sus variables "x" e "y", entonces:
F(x;y)= (ax+by)/(nx+my )=a/n=b/m
Para simplificar...
Se reduce a fracciones
simples
Aquellas fracciones
que tienen una o más
fracciones en...
Denominador
Numerador
FRACCIONES
PARCIALES
Operación de
descomposición
inversa a
la adición de
fracciones
Segundo
caso
Para resolver este caso, a cada factor
lineal de la forma ax + b que aparezca
repetido "n" veces en el denominador, le
corresponde una suma de fracciones.
En el denominador hay factores
lineales repetidos "n" veces.
Primer
caso
Para resolver este caso de la forma ax + b y que sea el denominador le corresponde una suma defracciones de la foma A/ax + b, A constante a determinar.
Denominador de
factores líneales
no repetidos
OBSERVACIÓN
FRACCIONES
EQUIVALENTES
Presentan el mismo valor
númerico para un conjunto
de valores admitidos por las
variables
FRACCIÓN
IRREDUCTIBLE
Sus términos son
expresiones algebraicas
primos entre si
SIMPLIFICACIÓN DE
EXPRESIONES
ALGEBRAICAS
Los factores comunes, al simplificarse
el MCD de los términos de la fracción
Factoriza el numerador y numerador,
después de lo cual se simplifican los
factores comunes
Transformar una fracción algebraica a
otra fracción equivalente irreductible
DEFINICIÓN
Numerador o denominador
conformado por una Expresión
Algebraica
División indicada de dos
polinomios
Q(x) polinomio
no constante
P(x) y Q(x)