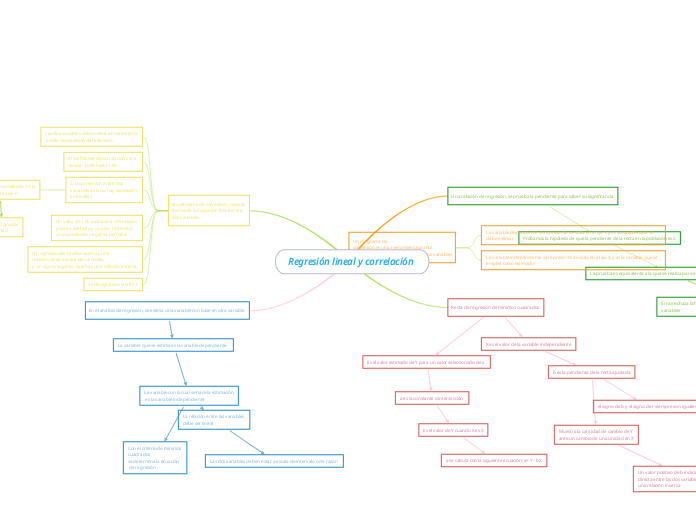
Regresión lineal y correlación
En el análisis de regresión, se estima una variable con base en otra variable
La variable que se estima es la variable dependiente
La variable con la cual se hace la estimación
es la variable independiente
Con el criterio de mínimos
cuadrados
se determina la ecuación
de regresión
La relación entre las variables
debe ser lineal
Las dos variables deben estar a escala de intervalo o de razón
el coeficiente de correlación mide la
fuerza de la asociación lineal entre
dos variables
Se designa con la letra r
Un signo positivo indica que hay una
relación directa entre las variables,
y un signo negativo, que hay una relación inversa
Un valor de 1.00 indica una correlación
positiva perfecta y uno de 1.00 indica
una correlación negativa perfecta
Si la correlacion entre dos
variables es 0, no hay asociación
entre ellas
Se determina si la correlación en la
población es distinta de 0
Con n -2 grados
de libertad
El coeficiente de correlación varia
desde -1.000 hasta 1.00
Las dos variables deben estar al menos en la
escala de medición del intervalo
Recta de regresión de mínimos cuadrados
Es el valor estimado de Y para un valor seleccionado de x
a es la constante o intersección
Es el valor de Y cuando X es 0
a se calcula con la siguiente ecuación: a= Y - bX
X es el valor de la variable independiente
b es la pendiente de la recta ajustada
Muestra la cantidad de cambio de Y
ante un cambio de una unidad en X
Un valor positivo de b indica una relación
directa entre las dos variables y un valor negativo,
una relación inversa
el signo de b y el signo de r siempre son iguales
Un diagrama de
dispersión es una herramienta grafica
para representar la relación entre dos variables
La variable independiente se representa a escala en el eje X, y es la variable que se emplea como estimador
La variable dependiente se representa a escala en el eje Y, y es la variable que se debe estimar
Una relación de regresión, se prueba la pendiente para saber su significancia
Probamos la hipótesis de que la pendiente de la recta en la población es 0
La prueba es equivalente a la que se realiza para el coeficiente de correlación
Si no rechaza la hipótesis nula, se concluye que no hay relación entre las dos variables
