por Pamela Minaya hace 3 meses
73
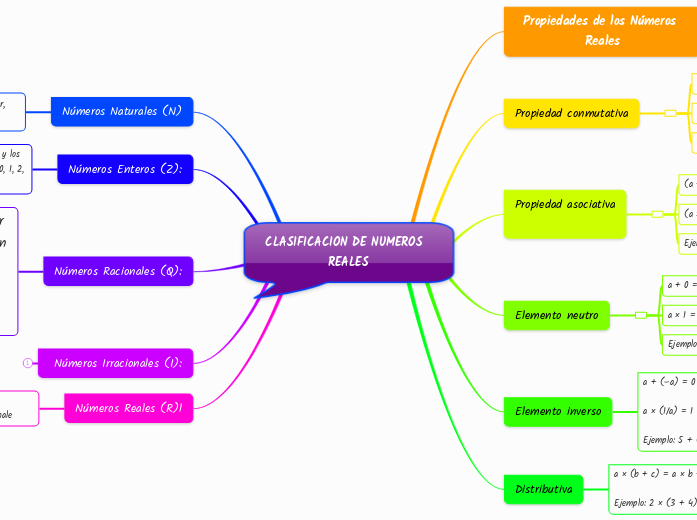
CLASIFICACION DE NUMEROS REALES
por Pamela Minaya hace 3 meses
73

A noun is a word that functions as the name of some specific thing or set of things, such as living creatures, objects, places, actions, qualities, states of existence, or ideas.
Compound nouns are words where two nouns have been stuck together to make a new noun. Compound nouns should be written as one word, without a hyphen.
Generic nouns are nouns that are part of a generic statement. Generic nouns can be singular or plural. The opposite of generic nouns is collective nouns.
The difference between definite/indefinite and generic nouns is that in the sentence there must be a blanket statement or question.
Proper nouns are the names of specific people or places. They should always begin with a capital letter.
A concrete noun is a noun that can be identified through one of the five senses (taste, touch, sight, hearing, smell).
Possessive nouns are nouns which possess something, normally another noun.