przez maria del carmen fernandez camacho 4 lat temu
493
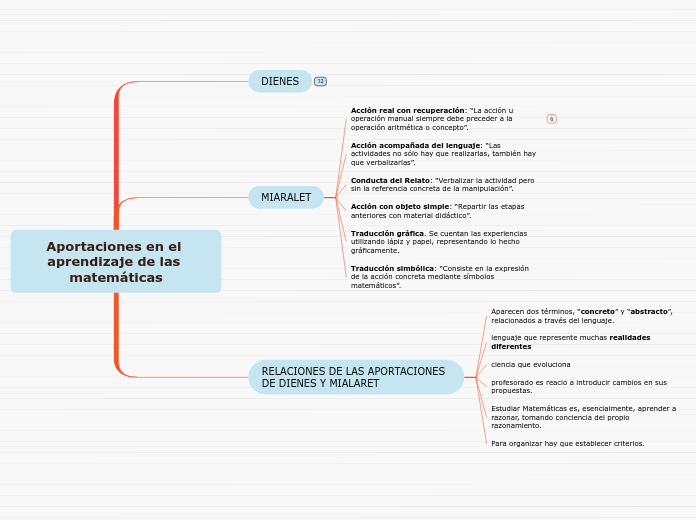
Aportaciones en el aprendizaje de las matemáticas
przez maria del carmen fernandez camacho 4 lat temu
493

Więcej takich
Other challenges
Challenges
Other
Main Goal
Character traits
Type of character