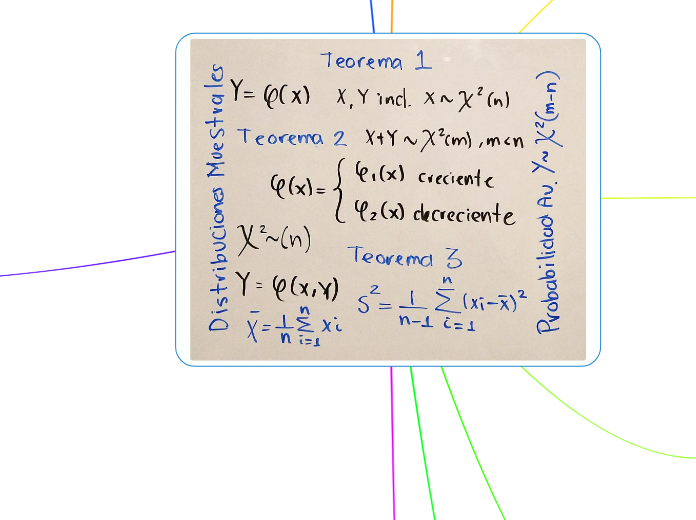
Esperanza Matemática y Estadísticos de Orden

Więcej takich

CONCEPTOS QUÍMICOS

przez isac zapata

Funcion Exponencial

przez Jean Pierre Yanez

Dominio, contradominio y rango

przez Citlalli González Sánchez

mapa mental trigonometria

przez sebastian acevedo

Fórmulas de los Estadísticos

Mediana

Rango

Varianza Muestral

Media Muestral

Proposiciones importantes de las distribuciones muestrales

Valor esperado y varianza

𝑠^2

X barra

Varianza

Esperanza

Estadístico

Un estadístico es cualquier función de la muestra, se dice que g(x1, x2, ..., xn) es un estadístico

Muestra Aleatoria

Una muestra aleatoria son variables aleatorias x1, x2, ..., xn que cumplen el ser independientes e idénticamente distribuidas.

Definición de los Vectores de Transformación

Cociente

𝑦/𝑥

(x, 𝑦/𝑥) o (𝑦/𝑥, y)

𝑥/𝑦

(x, 𝑥/𝑦) o (𝑥/𝑦, y)

Producto

xy

(xy, y) o (x, xy)

Resta

y-x

(y-x, y) o (x, y-x)

x-y

(x-y, y) o (x, x-y)

Suma

x+y

(x,x+y) o (x+y, y)

Tercer teorema de la transformación para vectores aleatorias

Tercer Teorema de Cambio de Variable

Def. Sea (X,Y) un vector continuo con valores en I⊆ℝ^2 y con función de densidad f(x,y). Sea φ(x,y): I→ℝ^2 una función continua con inversa φ^-1(u,v) diferenciable. Entonces el vector (U,V)=φ(x,y) toma valores en φ(I) y tiene función de densidad.

Paso 6: Hallamos la función de densidad que nos pide.

Paso 5: Hallamos el dominio de f(u,v).

Paso 4: Utilizando el Teorema, elaboramos la f(u,v).

Paso 3: Hallar las inversas respectivas.

Paso 2: Plantear el vector de transformación.

Paso 1: Identificar la f(x,y) y su dominio.

Segundo teorema de la transformación para variables aleatorias

Teorema de Cambio de Variable 2

Def. Sea X una variable aleatoria continua con valores dentro de un intervalo (a,b)∈ ℝ y con función de densidad f(x), entonces, si tenemos una φ(x) que sea creciente y decreciente para diferentes intervalos, se denotarán como φ1(x), φ2(x), respectivamente, cumpliendo que sean continuas, creciente y decreciente, y tengan inversas diferenciables, la función de densidad para la variable Y= φ(x) está dada por.

Primer teorema de la transformación para variables aleatorias

Teorema de Cambio de Variable 1

Def. Sea X una variable aleatoria continua con valores dentro de un intervalo (a,b) ∈ ℝ , y con función de densidad f(x). Sea φ: (a,b) →ℝ, una función continua, estrictamente creciente o decreciente y con inversa diferenciable. Entonces la variable aleatoria Y= φ(x), tiene la siguiente función de densidad con su dominio.