Fórmulas de los Estadísticos
Mediana
Rango
Varianza Muestral
Media Muestral
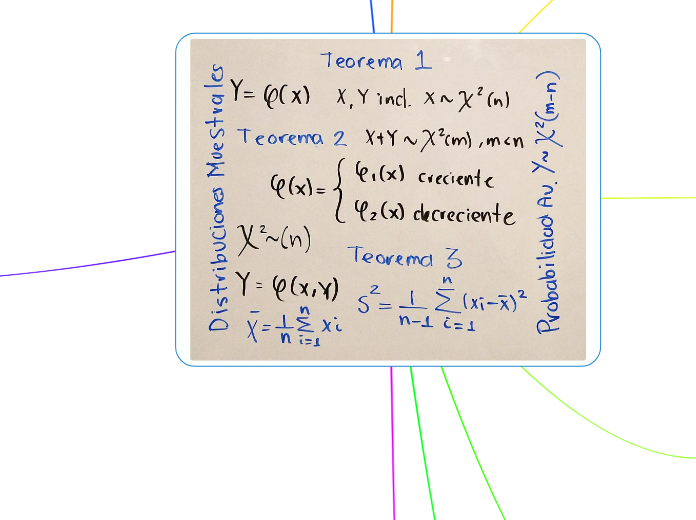
Proposiciones importantes de las distribuciones muestrales
Valor esperado y varianza
𝑠^2
X barra
Varianza
Esperanza
Estadístico
Un estadístico es cualquier función de la muestra, se dice que g(x1, x2, ..., xn) es un estadístico
Muestra Aleatoria
Una muestra aleatoria son variables aleatorias x1, x2, ..., xn que cumplen el ser independientes e idénticamente distribuidas.
Definición de los Vectores de Transformación
Cociente
𝑦/𝑥
(x, 𝑦/𝑥) o (𝑦/𝑥, y)
𝑥/𝑦
(x, 𝑥/𝑦) o (𝑥/𝑦, y)
Producto
xy
(xy, y) o (x, xy)
Resta
y-x
(y-x, y) o (x, y-x)
x-y
(x-y, y) o (x, x-y)
Suma
x+y
(x,x+y) o (x+y, y)
Tercer teorema de la transformación para vectores aleatorias
Tercer Teorema de Cambio de Variable
Def. Sea (X,Y) un vector continuo con valores en I⊆ℝ^2 y con función de densidad f(x,y). Sea φ(x,y): I→ℝ^2 una función continua con inversa φ^-1(u,v) diferenciable.
Entonces el vector (U,V)=φ(x,y) toma valores en φ(I) y tiene función de densidad.
Paso 6: Hallamos la función de densidad que nos pide.
Paso 5: Hallamos el dominio de f(u,v).
Paso 4: Utilizando el Teorema, elaboramos la f(u,v).
Paso 3: Hallar las inversas respectivas.
Paso 2: Plantear el vector de transformación.
Paso 1: Identificar la f(x,y) y su dominio.
Segundo teorema de la transformación para variables aleatorias
Teorema de Cambio de Variable 2
Def. Sea X una variable aleatoria continua con valores dentro de un intervalo (a,b)∈ ℝ y con función de densidad f(x), entonces, si tenemos una φ(x) que sea creciente y decreciente para diferentes intervalos, se denotarán como φ1(x), φ2(x), respectivamente, cumpliendo que sean continuas, creciente y decreciente, y tengan inversas diferenciables, la función de densidad para la variable Y= φ(x) está dada por.
Primer teorema de la transformación para variables aleatorias
Teorema de Cambio de Variable 1
Def. Sea X una variable aleatoria continua con valores dentro de un intervalo (a,b) ∈ ℝ , y con función de densidad f(x).
Sea φ: (a,b) →ℝ, una función continua, estrictamente creciente o decreciente y con inversa diferenciable. Entonces la variable aleatoria Y= φ(x), tiene la siguiente función de densidad con su dominio.