door William Sone 1 maand geleden
82
Quadratics
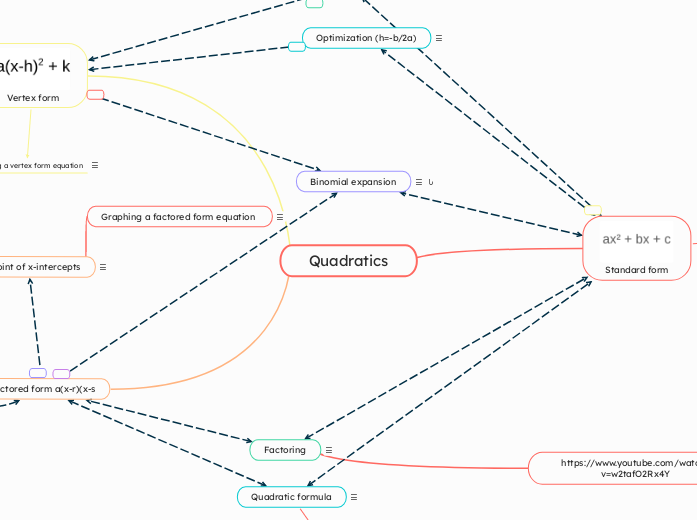
door William Sone 1 maand geleden
82

Quadratic formula is another way of converting an equation in standard form to an equation in factored form. Below is the quadratic formula.
x = b±√(b²-4ac))/(2a)
Below are the steps on how to use quadratic formula
Step 1: Substitute all the variables for the numbers in your equation except x into the formula.
Step 2: Solve for everything inside of the square root using BEDMAS.
Step 3: Now you must apply your equation into two scenarios. The first scenario is the square root being positive. Solve and get your first x-intercept. The second scenario is the square root being negative. Solve and get your second x-intercept.
Note: The equation may only have 1 or even 0 x-intercepts.
Step 4: Now that you have your x-intercept(s), flip the sign and place them in the brackets along with x. Remember to also include your stretch/compression factor.
Example: Your x-intercepts are 3 and -5 and your stretch factor is 3. This means, your equation will look like the equation below.
y = 3(x + 3)(x - 3)
Step 5: Congratulations, you have changed a standard form equation into a vertex form equation.
Factoring is one way to convert a standard form equation into a factored form equation. There are three types of expressions you can factor: simple trinomials, complex trinomials and special cases. For simple and complex trinomials, you must use the acronym MAN. Below is the process on how to use MAN.
M: Multiply: Multiple the "a" value by the c value
A: Add: Identify the b value
N: Numbers: You must find 2 numbers that multiply to the sum of the "a" and c value but also add to the b value
Simple trinomials
Simple trinomials have a stretch factor of only 1
Step 1: Use the acronym MAN
Step 2: Draw 2 brackets, one with x plus the first number you found in the N in MAN and another bracket with x plus the second number you found in the N in MAN.
Example: Your 2 numbers from the N in MAN are 6 and 2.
So your new expression will be (x+6)(x+2)
Step 3: Congratulations, you converted a standard form equation into a factored form equation.
Complex trinomials
Complex trinomials are trinomials the have an "a" more than 1. Below are steps on how to factor a complex trinomial
Step 1: Try to find a GCF for all 3 of the terms in the trinomial , if there is a GCF, factor it out and continue to the next step, if there is not, continue to the next step.
Step 2: Use the acronym MAN
Step 3: Once you found your 2 numbers for the N in MAN, substitute the b value for these 2 numbers with the variable. This process is known as decomposition
Example: The 2 numbers for the N in MAN are -6 and -5. The expression is 5n(squared) -11n + 6. So the new equation after decomposition is 5n(squared) - 5n -6n + 6.
Step 4: Now that there are 4 terms, separate them into 2 groups that you think will yield the largest GCF. Once you have the 2 groups, find the GCF of each group. Write the GCF in the space below. Than, divide each term by that GCF. The quotient must be written in a bracket multiplied by the GCF.
This process is known as factoring by grouping.
Example: =5n(squared) - 5n -6n -6
=5n(n-1) -6 (n-6)
Note: If the first term of one of the groups is negative, the GCF must be negative.
Step 5: The terms in each bracket should be the same, if not, go back to step 4.
Step 6: The next step is to make 2 brackets. One bracket should be for the GCFs found in step 4 and the other should be the value in both of the brackets.
Example: =5n(n-1)-6(n-1)
=(5n-6)(n-1)
Special cases
There are 2 types of special cases, difference of squares and perfect squares.
Difference of squares
A difference of square is an expression that has an x value squared that adds/subtracts an integer or an expression that has an integer that adds/subtracts an x-value squared. However, if an expression has addition, it is NOT FACTORABLE. Below is a shortcut on how to factor out a difference of square however, you can always use complex factoring.
Step 1: Square root the x value
Step 2: Square root the integer
Step 3: Your expression will be x plus the integer in the first bracket and x minus the integer in the second bracket.
Perfect squares
Perfect square expressions are expressions that, when factored out, form 2 identical brackets. Below is a shortcut on how to factor out a perfect square however, you can always use complex factoring.
Step 1: Identify the expression is a perfect square
Step 2: Draw a bracket below that includes x plus half the b value squared.
Example: = x(squared) + 8x + 16
=(x+4)(x+4) or (x+4) squared
Binomial expansion is the process in which you expand all the terms in 2 brackets beside each other. This process is extremely important for converting an equation from vertex or factored form to standard form.
The following steps below are on how to do binomial expansion using FOIL and are based on the example below.
(a + b)( c + d)
Step 1: Multiply a with c
Step 2: Multiply a with d
Step 3: Multiply b with c
Step 4: Multiply b with d
Below is a Youtube video to help explain FOIL
https://www.youtube.com/watch?v=EX18-4PjiUA
Special products
Not all binomial expressions have to be done using FOIL. Some have shortcuts that we can use. The two main special products are perfect squares and difference of squares.
Perfect squares
Perfect squares are when both brackets are the exact same value. For example (a + b) squared would be a perfect square. When dealing with perfect squares, you may use FOIL or you can use a special formula based on the example above. The special formula is below.
Difference of squares
A difference of squares is when there are 2 brackets beside each other with one bracket having x plus an integer and the second having x minus an integer. Both numbers must be the same distance from 0. For example, (x + 25)(x - 25). You may use FOIL or you can do the special method shown below.
Step 1: Multiply the x's together
Step 2: Multiply the integers together
Step 3: Put it all together
Example: (x+5)(x-5)
x(squared) - 25
How this all applies back to converting an equation from vertex or factored form to standard form.
Binomial expansion is essential for converting a factored or vertex form equation into a standard form equation. Now that you know binomial expansion, below are the steps on how to convert an equation from vertex or factored form into standard form.
Converting an equation from vertex form to standard form
Step 1: Use binomial expansion for the values inside the bracket (that being h and x). You may do this by using the Perfect square formula or FOIL.
Step 2: Use distribution of property to distribute the "a" value to all the terms inside the bracket.
Step 3: Simplify the expression
Step 4: Congratulations, you have converted a vertex form equation into a standard form equation!
Converting an equation from factored form to standard form
Step 1: Use binomial expansion on the brackets
Step 2: Use distribution of property to distribute the "a" value to all the terms inside the bracket.
Step 3: Simplify the expression
Step 4: Congratulations, you have converted a factored form equation into a standard form equation!
Optimization is a much faster way to convert a standard form equation into a vertex form equation. Below are the steps on how to use optimization.
Step 1: Solve for the x-value of the vertex by using the formula h=-b/2a. The h will be your x-value.
Example: h=-6/2(2)
h=- -1.5
Step 2: Solve for y by substituting the x-value to the original equation.
Step 3: Put the x and y value together and you have your vertex.
Step 4: Your x value of the vertex will be your h value in the vertex form equation. Simply switch the sign and substitute it for h.
Step 5: Your y value of the vertex will be your k value in the vertex form equation. Simply substitute k for the y value.
Step 6: Your stretch/compression factor will be your a value. Simply substitute "a" for the stretch/compression factor.
Step 7: Congratulations, you have officially converted a standard form equation into a vertex form equation!
Below is a Youtube video to help explain the concept:
https://www.youtube.com/watch?v=0Jz5lXgGIMo
Completing the square is one way to find the vertex of a standard form equation. Below are the steps on how to complete the square.
Step 1: Factor out the "a" value from the standard form equation.
Step 2: Divide the b value by 2a. Then square it.
Step 3: The answer you just got from step 2 must be put in the bracket as a positive and negative value to cancel eachother out
Example: If the value from step 2 is 16, than it must be written in the bracket as (+16-16)
Step 4: Multiply the "a" value by the negative value of the answer you got from step 2 inside the bracket. Move this new value outside the bracket.
Step 5: Simplify the equation by factoring
This process is complicated. For further information on completing the square. Please see this Youtube video below:
https://www.youtube.com/watch?v=a7WJRrRuSTc
The factored form of an equation tells us the x intercepts of the parabola. Below are the steps on how to find the vertex of a factored form equation. This is necessary to graph this type of equation and to convert this equation from factored form to vertex form.
Step 1: Find the x-intercepts of the factored form equation by solving for x in each of the brackets by making 2 equations that equal 0.
Example: y =-1/2 (x-5)(x+3)
x-5=0 x+3=0
x=5 x=-3
Step 2: Find the axis of symmetry of the parabola by adding the x-intercepts together and dividing that by 2.
Step 3: Find the value of y by subbing your axis of symmetry value into x.
Example: y = -1/2 ((1)-5)((1)+3)
y = -1/2 (-4)(4)
y = -1/2 (-16)
y = 8
Step 4: The axis of symmetry value is the x in your vertex and the y value you just found in step 3 is your y value in your vertex. Put the together into (x,y) and that is your vertex!
Now that you have the vertex of the equation from the previous section, you can now start to form your new vertex form equation! Below are the steps on how to do that.
Step 1: Identify the vertex form of an equation
Step 2: Your x value of the vertex will be your h value in the vertex form equation. Simply switch the sign and substitute it for h.
Step 3: Your y value of the vertex will be your k value in the vertex form equation. Simply substitute k for the y value.
Step 4: Your stretch/compression factor will be your a value. Simply substitute "a" for the stretch/compression factor.
Step 5: Congratulations, you have officially converted a factored form equation into a vertex form equation!
Now that you have the x intercepts and the vertex from the previous section, simply plot all of those points, connect the points and you have a graph from that equation!
Below is a Youtube video to help explain how to graph a factored form equation:
https://www.youtube.com/watch?v=EV57jv7JKCs
In order to change a vertex form equation into a factored form equation. You can change the equation to standard form and then factor it or use quadratic formula or you can solve for zeros which is shown below.
Step 1: Substitute y for 0
Step 2: Get rid of the "a" value by dividing both sides of the equation.
Step 3: Set up the equation for two scenarios. One where the square root of the bracket is positive and one where the square root of the bracket is negative. Solve for both of the scenarios.
Note: There may only be 1 or no x-intercepts
Step 4: Set up your new factored form equation by creating two brackets. One with an x-intercept and x and another with an x-intercept and x. You also must substitute "a" for the stretch/compression factor.
Example: Your x-intercepts are 3 and -5 and your stretch factor is 3. This means, your equation will look like the equation below.
y = 3(x + 3)(x - 3)
Step 5: Congratulations, you changed a vertex form equation into a factored form equation.
A vertex form equation tells us the vertex of a parabola. Below are the steps on how to graph a vertex form equation.
Step 1: Identify the vertex of the parent function vertex (0,0)
Step 2: Look at the h value in the bracket, if it is negative, translate the vertex (0,0) to the right however many spaces it says. If the h value is positive, translate the vertex (0,0) to the left however many spaces it says. The h value represents the x value of the vertex of your equation.
Step 3: Look at the k value. The k value is the y value of the vertex of your equation.
Step 4: Put the x and y values of the vertex together into (x,y). This coordinate is your vertex of the equation!
Step 5: Look at the "a" value of the equation, this is your stretch/compression factor. Create a table of values with the x values -4,-3,-2,-1,0,1,2,3,4. Square each of these values and then multiply them by the stretch/compression factor. This will give you the y values.
Step 6: From the table of values, select good points with whole y values rather than decimals. If you feel there aren't enough good points, extend your table of values by adding more x values.
Step 7: Finally, you can start to graph your equation. Plot your vertex and look for all the good points on your table of values. From the vertex, your next point should be however many spaces to the right if the x value is positive, and however many spaces to the left if the x value is negative. Then the point must be moved however many spaces down is the y value is negative and however many spaces up if the y value is positive. Continue this process with all the good points. Remember, THE POINTS ON THE TABLE OF VALUES CANNOT BE PLOT AT FACE VALUE UNLESS THE VERTEX OF YOUR EQUATION IS (0,0)
REMEMBER: If a vertex form equation is missing an h or k value, assume the value is 0. If a vertex form equation is missing an "a" value, assume the value is 1.
Here is a Youtube video to help explain how to graph a vertex form equation:
https://www.youtube.com/watch?v=TxPDQfWeAUg
In order to graph an equation in standard form, you have 2 options.
1: Change the equation to vertex or factored form
2: Create a table of values with the x values -4,-3,2,1,0,1,2,3,4 and plug them into your equation to solve for the y values. If there aren't enough points on the table, extend it!